Explaining Psychological Statistics 4th Edition Chapter 9 Exercises
Now that we have the background that we need in descriptive statitstics and probability theory, we'll begin talking about inferential statistics.
In other words, we want to be able to make claims about populations based on samples.
- example: We might ask about the value of knowing about statistics. - Suppose that we think that knowing about statistics helps people understand the USA Today newspaper. - So we take a sample of students who have completed this class, and a sample of students from another class (none of whom have had a statitstics course). - Each person is given a copy of the paper, asked to read it, and are later tested for their comprehension of the stories in the paper.
- - what are the populations here?
- 1) students who take stats 2) students who don't take stats
- problem: is this 4% difference "real" or is it just due to sampling error.
- If it is "real" then we can conclude that the two populations are different, and that there is support for our hypothesis that stats helps with reading the paper If the difference is due to sampling error, then we should conclude that the populations are (probabily) the same, and further that stats knowledge doesn't help with understanding the paper
Okay, let's formalize this procedure.
- The advantance of "formalizing" the procedure, is that if everyone uses the same techniques, then we know why they conclude what they do, and furthermore, we know about the assumptions that they are making
Hpothesis testing - the big picture view (more details will follow)
- step1: Make a hypothesis and select a criteria for the decsion
- - your hypothesis is an educated guess/prediction about the effect of particular events/treatments/factors (which result in differences between populations) - your hypothesis may be general (e.g., this course will change comprehension abilities), or specific (e.g., this course will improve comprehension abilities by at least 10%).
- - randomly select individuals from a population - randomly assign selected individuals to specific treatment groups
- (note that in our example above we didn't do this, we assigned individuals to groups based on their past experiences. As a results our conclusions could be compromised, maybe the people who take stats are generally people who have better comprehension abilities, and so taking stats didn't have anything to do with their performance on the test)
- - things like z-scores, t-tests, f-tests (ANOVA)
- - roughly, how likely is this difference due to sampling error? Given this probability, what should we conclude?
Let's look at each of these steps in more detail
- Step1: Make a hypothesis and select a criteria for the decsion The standard logic that underlies hypothesis testing is that there are always (at least) two hypotheses: the null hypothesis and the alternative hypothesis
- The null hypothesis (H0) predicts that the independent variable (treatment) has no effect on the dependent variable for the population.
The alternative hypothesis (H1) predicts that the independent variable will have an effect on the dependent variable for the population - we'll talk more about how specific this hypothesis may be
- Why?
- Generally, It is easier to show that something isn't true, than to prove that it is. This is especially true when we are dealing with samples. Remember that we aren't testing every individual in the population, only a sub set.
- Hypothesis: All dogs have 4 legs.
- to reject: need to have a sample which includes 1 or more dogs with more or fewer than 4 legs. to accept: need to examine every dog in the population and count their legs
So part of the first step is to set up your null hypothesis and your alternative hypothesis
The other part of this step is to decide what criteria that you are going to use to either reject or fail to reject (not accept) the null hypothesis
- So consider the problem that we have. We have a sample and its descriptive statistics are different from the population's parameters (which may be based on the control group sample statistics). How do we decide whether the difference that we see is due to a "real" difference (which reflects a difference between two populations) or is due to sampling error?
To deal with this problem the researcher must set a criteria in advance.
- For example, think of the kinds of questions we were asking in the previous chapter. Given a population X with a m = 65 and a s = 10, what is the probability that our sample (of size n) will have a mean of 80? We're going to be asking the same questions here, but taking it a step further and say things like, "Gee, the probability that my sample has a mean of 80 is 0.0002. That's pretty small. I'll bet that my sample isn't really from this population, but is instead from another population."
setting a criteria in advance is concerned with this part about saying "that's pretty small". When we set the criteria in advance, we are essentially saying, how small a chance is small enough to reject the null hypothesis. Or in other words, how big a difference do I need to have to reject the null hypothesis.
- note: often this is determined by convention within your own discipline. For example, some fields may say that p < 0.05 is low enough to reject the H0. While other feilds may chose p < 0.01 as the cut off.
That's the big picture of setting the criteria, now let's look at the details
- what are the possible real world situations?
- - H0 is correct
- H0 is wrong
- - H0 is correct
- H0 is wrong
- - 2 ways of making mistakes
- 2 chances to be correct
| Actual situation | |||||||||||||
| Experimenter's Conclusions |
|
- the two kinds of error each have their own name, because they really are reflecting different things
type I error (a, alpha) - the H0 is actually correct, but the experimenter rejected it
- - e.g., there really is only one population, even though the probability of getting a sample was really small, you just got one of those rare samples
type II error (b, beta)- the H0 is really wrong, but the experiment didn't feel as though they could reject it
- - e.g., your sample really does come from another population, but your sample mean is too close to the original population mean that you aren't can't rule out the possibility that there is only one population
| Actual situation | |||||||||||
| Jury's Verdict |
|
- Type I error - sending an innocent person to jail
Type II error - letting a guilty person go free
In scientific research, we typically take a conservative approach, and set our critera such that we try to minimize the chance of making a Type I error (concluding that there is an effect of something when there really isn't). In other words, scientists focus on setting an acceptible alpha level (a), or level of significance.
The alpha level (a), or level of significance, is a probabiity value that defines the very unlikely sample outcomes when the null hypothesis is true. Whenever an experiment produces very unlikely data (as defined by alpha), we will reject the null hypothesis. Thus, the alpha level also defines the probability of a Type I error - that is, the probability of rejecting H0 when it is actually true.
- note: In psychology a is usually set at 0.05
Consider the following sample mean distributions.
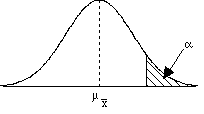 | a = prob of making a type I error |
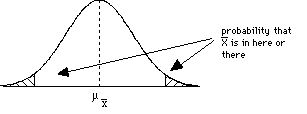 | general alternative hypothesis H0: no difference H1: there is a difference Two-tailed test |
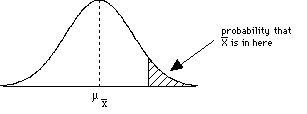 | specific alternative hypothesis
H1: there is a difference & the new group should have a higher mean One-tailed test |
so how do we interpret these graphs?
- If our sample mean falls into the shaded areas then we reject the H0. On the other hand, if our sample mean falls outside of the shaded areas, then we may not reject the H0. These shaded regions are called the critical regions .
The critical region is composed of extreme sample values that are very unlikely to be obtained if the null hypothesis is true. The size of the critical region is determined by the alpha level. Sample data that fall in the critical region will warrant the rejection of the null hypothesis.
Population distribution 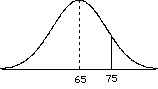 | So the population m = 65 and s = 10.
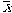 = 69. = 69. Did the treatment work? Does it affect the population of individuals? Which distribution should you look at? |
distribution of sample means 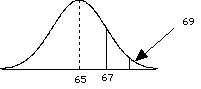 | Look at distribution of sample means. Find your sample mean in the distribution. Look up the probability of getting that mean or higher for the sample (see last chapter). Let's assume an a = 0.05 now we need to find our standard error. |
| | what is our critical region? Well, this is a one tailed test. so, look at the unit normal table, and find the area that corresponds to a = 0.05 z = 1.65 (conservative, really 1.645) so, translate this into a sample mean = Z  + m = (1.65)(2)+65 = 68.3 + m = (1.65)(2)+65 = 68.3so, if = 69, then we reject the H0 |
Another way that we could have done this question is just to use z-scores.
- since we know that the z-score corresponding to the critical region is 1.65, then we just need to compute the z-score corresponding to the sample mean to see if it is higher or lower than this critical z-score.
Z ![]() =
=  = (69 - 65) / 2 = 2.0 since > Zcritical, then we can reject the H0
= (69 - 65) / 2 = 2.0 since > Zcritical, then we can reject the H0
However, the most common way to do hypothesis testing is to make a more general hypothesis, that the treatment will change the mean, either increase or decrease.
Population distribution 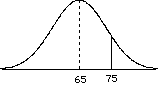 | So the population m = 65 and s = 10. Suppose that you take a sample of n = 25, give them the treatment and get a 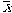 = 69. Did the treatment work? Does it affect the population of individuals? = 69. Did the treatment work? Does it affect the population of individuals? Which distribution should you look at? population? |
distribution of sample means 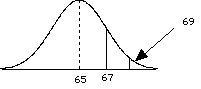 | Look at distribution of sample means. Find your sample mean in the distribution. Look up the probability of getting that mean or higher for the sample (see last chapter). Let's assume an a = 0.05 |
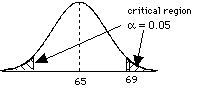 | now we need to find our standard error.  = =  = 10/(sqroot 25) = 2 = 10/(sqroot 25) = 2 what is our critical region? Well, this is a two tailed test. |
Assumtions of hypothesis testing
- 1) Random sample - the samples must me representative of the populations. Random sampling helps to ensure the representativeness.
2) Independent observations -also related to the representativeness issue, each observation should be independent of all of the other observations. That is, the probability of a particular observation happening should remain constant.
3) s is known and is constant - the standard deviation of the original population must stay constant. Why? More generally, the treatment is assumed to be adding (or subtracting) a constant from every individual in the population. So the mean of that population may change as a result of the treatment, however, recall that adding (or subtracting) a constant from every individual does not change the standard deviation.
4) the sampling distribution is relatively normal - either because the distribution of the raw observations is relatively normal, or because of the Central Limit Theorem (or both).
Violations of any of these assumptions will severly compromise any conclusions that you make about the population based on your sample (basically, you need to use other kinds of inferential statistics that can deal with violations of various assumptions)
Almost done, but we need to talk a bit about the other kind of error that we might make
- recall:
| Actual situation | |||||||||||||
| Experimenter's Conclusions |
|
Type II error (b)- the H0 is really wrong, but the experiment didn't feel as though they could reject it
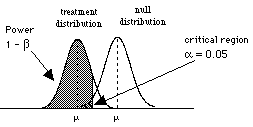
The power of a statistical test is the probability that the test will correctly reject a false null hypothesis. So power is 1 - b.
So, the more "powerful" the test, the more readily it will detect a treatment effect.
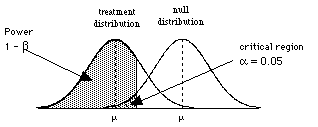
So to consider power, we need to consider the situation where H0 is wrong, that is when there are two populations, the treatment population and the null population
Power is the probability of obtaining sample data in the critical region when the null hypothesis is false.
So when there are two populations, the power will be related to how big a difference there is between the two.
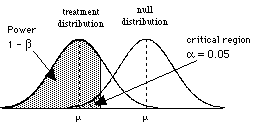 | a big difference between the two populations notice that the shaded region is large the chance to correctly reject the null hypothesis is good |
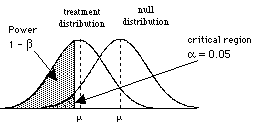 | a smaller difference between the two populations notice that the shaded region is smaller the chance to correctly reject the null hypothesis is not nearly as good |
Factors that affect power
- 1) Increasing a increases power.
2) One-tailed tests have more power than two-tailed tests, given that you have specified the correct tail.
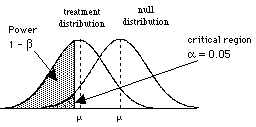 | One-tailed test a = 0.05 all of the critical region (a) is on one side of the distribution |
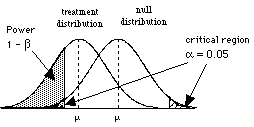 | Two-tailed test a = 0.05 because a specific direction is not predicted, the critical region (a) is spread out equally on both sides of the distribution as a result the power is smaller |
3) Increasing sample size increases power by reducing the standard error.
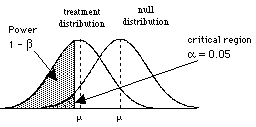 | Small n a = 0.05 relatively large standard error |
 | Larger n a = 0.05 Smaller standard error as a result the power is greater |
Explaining Psychological Statistics 4th Edition Chapter 9 Exercises
Source: https://psychology.illinoisstate.edu/jccutti/psych240/chpt8.html
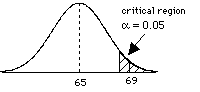
0 Response to "Explaining Psychological Statistics 4th Edition Chapter 9 Exercises"
Post a Comment